Interest Rates and Marginal Return on Capital

This is a simple model of capital. There are two commodities which are land and corn, but start with just a model of the corn. The numbers are not intended to be realistic, merely illustrative of the general concept.

Piecewise Linear Corn Model

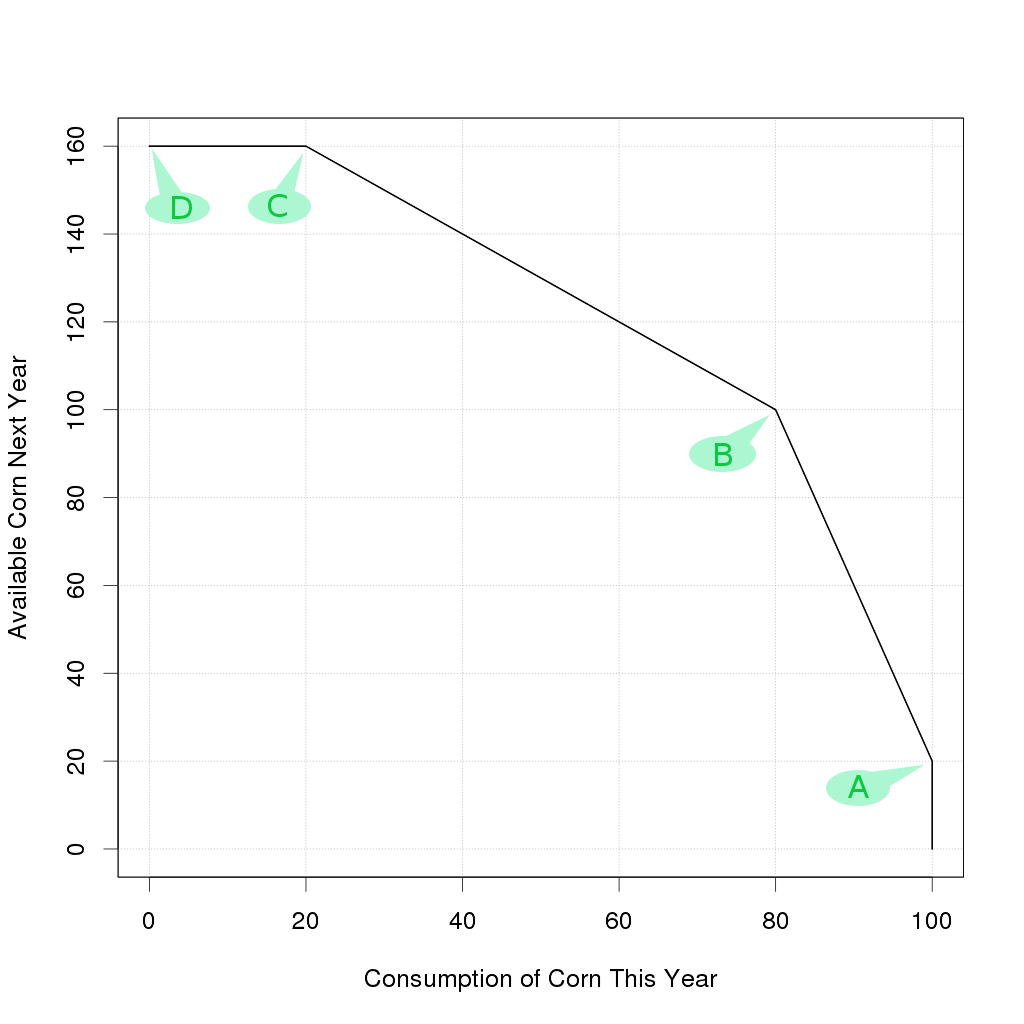
Linear models are an excellent starting point for most applied mathematics, however a purely linear model of capital has the problem that it cannot demonstrate diminishing returns and worse, there is no basis for making real decisions. A piecewise linear model is easy enough to explain, and it fits a physical story quite nicely to illustrate decision making.

Drawn above is a basic model, various key points are marked with letters, and these are explained below. This style of diagram is often called, an Irving Fisher diagram.

Key Point "A" -- Maximum Short-Tem Consumption

At this point we have current consumption at 100% so all the available corn is consumed. This also consumes the "seed corn" that is required to start next year's crop so as a consequence the harvest next time around is quite poor (only 20% of what the harvest was this year). It should be obvious that by continuously consuming the "seed corn" harvests will be consistently poor and the food supply will shrink.

Key Point "B" -- Maximum Long-Term Consumption

At this point, as much "seed corn" has been saved to get the biggest possible harvest from the land. However, exactly that amount has been saved and not a grain extra.

Region "AB" -- Productivity of Seed Corn

It should be evident that storing seed corn is a useful thing to do, but it is important to note the way this shows in the diagram. The gradient of the line AB is steep, thus by sacrificing only 20% of our consumption now, we gain an additional 80% consumption next year. That means each additional 1 unit of seed corn investment pays back 4 units of corn next year. The effective equivalent "interest rate" in physical terms is 300% per annum.

Key Point "C" -- Maximum Possible Storage

At this point people are consuming only 20% of the harvest this year and storing 80% for next year. When next year comes around some of that stored grain is planted as seeds and the remainder is available for additional consumption. This type of storage is just plain stockpiling, what you put in is exactly what you get out again.

Region "BC" -- Productivity of Warehousing

The gradient of the line in this region is less steep. Actually, this region makes neither gain nor loss and the effective equivalent "interest rate" in physical terms is 0% ... or no interest at all.

It's fair to point out that the zero interest rate does not imply people will never store any corn, they may be worried about future famine or they may just not be hungry right now. Personal preference assigns a percieved value to the corn that is not intrinsic to the corn itself. If it does turn out there is a famine next year, then a lot of hungry people will percieve a pound of corn to be far more important to them than the same pound of corn was during times of plenty.

People can make a profit out of this shift in perception by exchanging corn for something else in a multi-dimensional economy... but for the time being we don't have anything else in the economy. So let's ignore the idea of trade for the moment.

Important point to remember: the gradient at "AB" is steep, and the gradient at "BC" is less steep, thus implying a diminishing marginal return on capital as we cross point "B". This diminishing return becomes the absolutely criticial issue later on.

Key Point "D" -- Overproduction and Under Consumption

Reaching point "D" demonstrates that the warehouse can only hold so much, and beyond that the remainder cannot be stored. People are literally throwing away the corn where it either rots, or is eaten by rats. Of course, there wouldn't really be such a sharp corner at "D" but this is just a piecewise linear model so for simplicity please accept that the warehouse holds a fixed amount. Once again, this is illustrative of diminishing marginal returns on capital investment, thus, although the sharp corner here is not realistic, diminishing return in some form or other would be expected in a real economy.

Region "CD" -- Wastage

This horizontal region is where additional attempts at saving are a complete waste. There is nowhere to save and people are just throwing away resources. Interest rates here are actually lower than zero, indeed effectively we have an interest rate of negative 100% and this makes sense if you think about it. Suppose one person, for whatever reason wanted to borrow corn at the same time other people are throwing it away... this person could just ask for some, or pick up the bag of corn that another man left out in the street.

The going rate of interest in such a situation would be not only to pay no interest at all, but don't even bother paying back the principle.

Two-Person Equilibrium Model

People have personal preferences, the Production Possibilities Frontier drawn above explains how the physical system works, but it does not explain what people will do. Each person might make a decision about consumption vs saving, and various people will very likely make various decisions.

To explore this situation, consider two people "Careful Cauliflower" and "Fearless Freddy", each of which owns an equal size parcel of land. Freddy decides to consume 90% of his produce and save 10% as "seed corn" for next year, while Cauliflower is nervous about possibly running out of corn, so she consumes only 60% of her produce and saves a big 40%. Each of these people ends up sitting at their own personal equilibrium point at the start of the planting season, so we have two red dots on the following diagram.

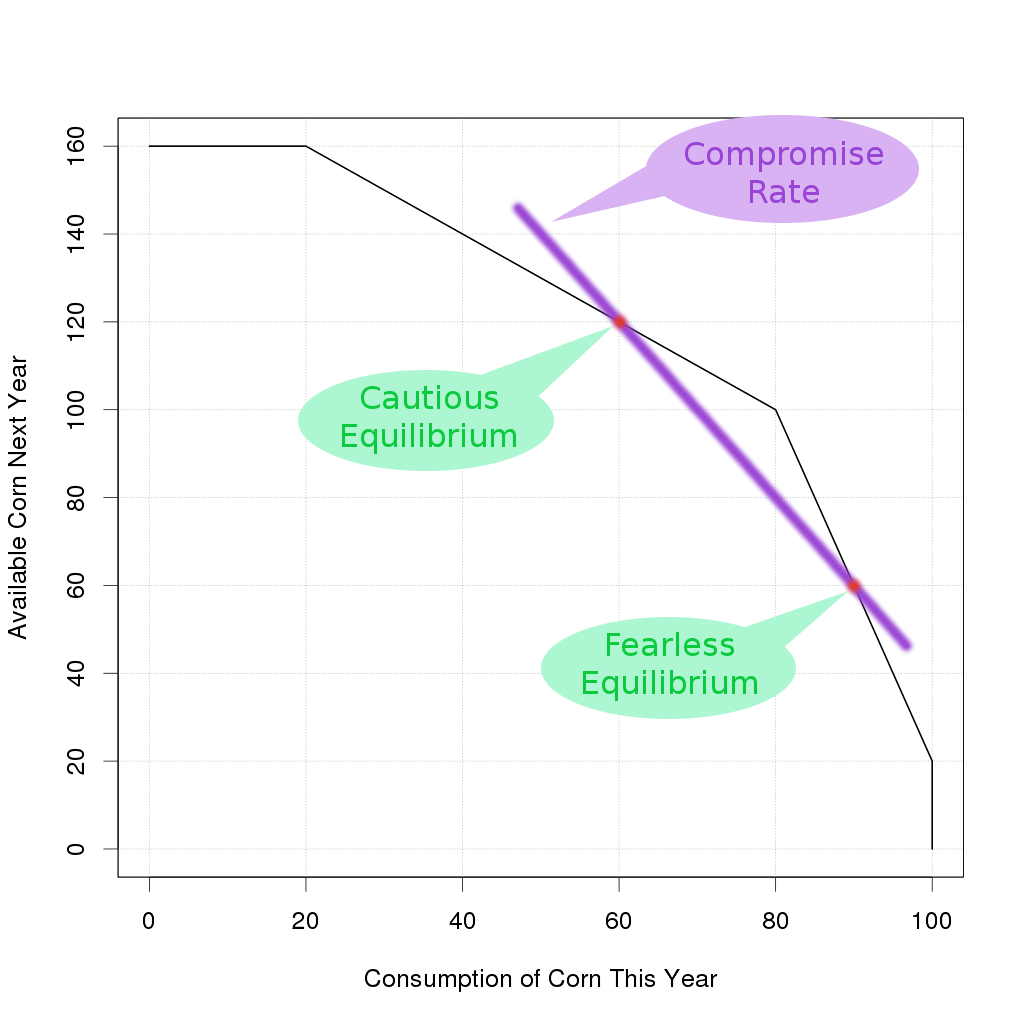
When planting gets underway, Fearless Freddy runs out of seeds halfway through and thinks to himself, "Oh crap! I need more seeds, I know what to do, I'll go over to Cauliflower's house and ask her for seeds, because she always keeps plenty."

So over he goes. Cautious Cauliflower has finished her planting and has a pile of corn left over, but she doesn't want to just give it away. She offers to lend her corn to Freddy with a demand that he pay some interest. For argument sake, suppose the two of them come to a compromise over the interest rate.

Note that with the equilibrium point that Cauliflower is sitting on, her effective physical interest rate is 0%. That is to say, she could choose to store the corn and get the same corn back at 0% interest rate, but by choosing to lend to Freddy at a compromise interest rate she gets a better return. On the other hand, Freddy is sitting at a different equilibrium point on the Production Possibilities Frontier so from his perspective, every unit of corn that he borrows from Cautious Cauliflower will pay back an effective return of 300%, and that's much higher than their compromise interest rate. Both parties are happy! It's a win/win trade here.

It gets more complicated, suppose one party wants to drive a hard bargain? We know that Cautious Cauliflower will never lend at a lower interest rate than 0% because based on her personal equilibrium point, she already is guaranteed to get 0% by the physical situation. We know that Fearless Freddy will not borrow at a higher interest rate than 300% because if he did that, even after planting and pulling in a larger harvest he would be worse off. Between those two extreme limits (which are set by the physical productivity of the corn), the two of them can duke it out.

But suppose there were a whole bunch of Cautious Cauliflowers spread at various points along the "BC" interval. Suppose there were also a whole bunch of Fearless Freddies spread at various points along the "AB" interval. How could they get together and start an auction that was sufficiently fair that the parties were still willing to trade, and also satisfied the needs of as many people as possible?

In effect, what happens is that the corner at "B" is not as sharp as what this simplified piecewise linear model pretends. We really have a more rounded corner. As the various parties auction between each other, they collectively get to an equilibrium point somewhere along that rounded corner, at which point the first derivative does determine the interest rate. The preferences of the parties concerned, and their method of negotiation ends up controlling where that equilibrium point lands along the curve.

Conclusions

Funtamentally, you can't avoid the relationship of interest rates and physical productivity. However, if anyone says "The return on capital is r, and r is a constant," what this person is implying is that the Production Possibilities Frontier is a very simple straight-line model, and further they are implying that no diminishing marginal return on capital exists. By imposing a simple linear model of capital, it no longer makes the slightest difference where the equilibrium point sits -- interest rates will be constant and that's all there is to it.

However, once we have a nonlinear model of capital, and diminishing returns do exist, suddenly that equilibrium point becomes all important! Moving the equilibrium to a different part of the curve implys different mechanisms are coming into play, and different decisions are being made. This is the place where individual preverences become significant. This is also the place where individual can trade with one another for mutual profit, and by making those trades we get a collective equilibrium determined by the marketplace.

Reference

Future

I mentioned two commodities, "land" and "corn", but so far the land is fixed and never trades.

Bringing land trades into the picture makes things more interesting... another day perhaps.

Consumption, Saving, Interest Rates and Capital